Speeding up a Sudoku solver with GEPA `optimize_anything`
February 21, 2026 by Marius Vach
A couple of days ago, Lakshya Agrawal and the team released a new version of [GEPA](https://gepa-ai.github.io/gepa/blog/2026/02/18/introducing-optimize-anything/), their awesome prompt optimizer, which now allows optimizing virtually every text-based artifact. It was already possible before, but now the API for basically "optimizing anything" is much more streamlined and intuitive.
I am very excited for this release and of course I had to take it out for a spin.
Some months ago I built a simple Sudoku solver with constraint propagation and backtracking, mostly for educational purposes, because I wanted to know how these kinds of solvers work.
So when I thought about what project I should use to try out GEPA, trying to optimize my very crude Sudoku solver was a very natural fit.
The idea is simple: you provide a seed artifact (the initial version of what you want to optimize) and an evaluate function that runs it and returns a score plus what they call "Actionable Side Information (ASI)" — detailed diagnostic feedback like runtimes, error messages, or correctness info. GEPA uses this to iteratively improve the artifact via an LLM. So we need three things:
* A seed artifact — our initial Sudoku solver
* A dataset, just like in classical ML
* An evaluation metric — correctness + solve time
There are lots of Sudoku datasets out there. I'm using this one from Hugging Face: https://huggingface.co/datasets/sapientinc/sudoku-extreme
## Load the dataset
```python
import pandas as pd
# Load a sample from the test set (smaller, 423k rows)
url = "https://huggingface.co/datasets/sapientinc/sudoku-extreme/resolve/refs%2Fconvert%2Fparquet/default/test/0000.parquet"
df = pd.read_parquet(url)
print(f"Loaded {len(df)} puzzles")
print(f"Rating range: {df['rating'].min()} - {df['rating'].max()}")
print(f"Columns: {list(df.columns)}")
df.head()
```
```python
# Sample a small dataset for GEPA: 200 train + 50 val, stratified by difficulty
hard = df[df['rating'] >= 50].sample(n=min(150, len(df[df['rating'] >= 50])), random_state=42)
medium = df[(df['rating'] >= 10) & (df['rating'] < 50)].sample(n=50, random_state=42)
easy = df[df['rating'] < 10].sample(n=50, random_state=42)
train_df = pd.concat([hard[:100], medium[:35], easy[:35]]).reset_index(drop=True)
val_df = pd.concat([hard[100:], medium[35:], easy[35:]]).reset_index(drop=True)
# Add AI Escargot to validation set
ai_escargot = {'source': 'ai_escargot', 'question': '8..........36......7..9.2...5...7.......457.....1...3...1....68..85...1..9....4..',
'answer': '812753649943682175675491283154237896369845721287169534521974368438526917796318452', 'rating': 999}
val_df = pd.concat([val_df, pd.DataFrame([ai_escargot])], ignore_index=True)
print(f"Train: {len(train_df)} puzzles, Val: {len(val_df)} puzzles")
print(f"Train rating stats:\n{train_df['rating'].describe()}")
print(f"\nVal rating stats:\n{val_df['rating'].describe()}")
```
```
Train: 170 puzzles, Val: 81 puzzles
Train rating stats:
count 170.000000
mean 45.864706
std 31.113068
min 0.000000
25% 22.000000
50% 52.500000
75% 63.000000
max 160.000000
Name: rating, dtype: float64
Val rating stats:
count 81.000000
mean 64.691358
std 112.174378
min 0.000000
25% 16.000000
50% 53.000000
75% 77.000000
max 999.000000
Name: rating, dtype: float64
```
AI Escargot is a sudoku puzzle by the Finnish mathematician Arto Inkala, which is often considered to be the hardest sudoku puzzle out there. I just wanted to make sure that it is also in the validation dataset, so I added it manually.
As I said, I already wrote a Sudoku solver back a couple months ago. I won't go over it here in detail. It really wasn't meant to be fast in any way. It was more optimized for clarity and for educational purposes. So there should be a lot of low-hanging fruit to optimize the speed of this solver. Here is a short excerpt:
## Sudoku solver
Here is a short excerpt of the seed solver. Full code: [GitHub Gist – `sudoku_solver_seed.py`](https://gist.github.com/vacmar01/7b7a8bd3d77795967deddd7a08b40718).
```python
import numpy as np
from collections import defaultdict
def puzzle_to_grid(puzzle_str):
return np.array([int(c) if c != '.' else 0 for c in puzzle_str]).reshape(9, 9)
def solve_backtrack(grid):
# uses naked singles + hidden singles + recursive backtracking
...
def solve(puzzle_str):
return grid_to_string(solve_backtrack(puzzle_to_grid(puzzle_str)))
```
## `evaluate` function
Okay, so now we have our seed candidate and a dataset split into training and validation. Now we get to the heart of it: an evaluation function that takes a candidate (our solver code) and one example (a row from the dataset), executes the code, and captures useful diagnostics like runtime plus compile/runtime errors. It returns a float score together with a dictionary containing additional information.
```python
import time
import traceback
def evaluate(candidate, example):
# 1. Exec the candidate into an isolated namespace
namespace = {}
try:
exec(candidate, namespace)
except Exception as e:
return 0.0, {"error": f"Compile error: {traceback.format_exc()}", "correct": False, "time": None}
solve_fn = namespace.get('solve')
if solve_fn is None:
return 0.0, {"error": "No 'solve' function defined", "correct": False, "time": None}
puzzle = example['question']
expected = example['answer']
# 2. Time the solve
try:
start = time.perf_counter()
result = solve_fn(puzzle)
elapsed = time.perf_counter() - start
except Exception as e:
return 0.0, {"error": f"Runtime error: {traceback.format_exc()}", "correct": False, "time": elapsed if 'elapsed' in dir() else None}
# 3. Check correctness — wrong answer = 0, no matter what
correct = (result == expected)
if not correct:
return 0.0, {"correct": False, "time": elapsed,
"got": result[:20] if result else None,
"expected": expected[:20]}
# 4. Score: time component (scaled so 10ms = 0, instant = 1)
time_score = max(0.0, 1.0 - elapsed * 100)
# 5. Small brevity bonus
num_lines = len(candidate.strip().splitlines())
brevity_score = 1.0 / num_lines
# 6. Weighted combination: 85% speed, 15% brevity
score = 0.85 * time_score + 0.15 * brevity_score
return score, {"correct": True, "time": elapsed, "num_lines": num_lines,
"time_score": round(time_score, 4),
"brevity_score": round(brevity_score, 4)}
```
As you can see we execute the string as python code and then run the solve function, while capturing either compilation errors, a missing `solve` function or any runtime errors. Then we'll measure the time it took to run with `time.perf_counter()` and construct a score from the runtime as well as a little regularization term from the lines of code (85% time and 15% LoC).
Let's take the function for a spin:
```python
from urllib.request import urlopen
seed_solver_url = "https://gist.githubusercontent.com/vacmar01/7b7a8bd3d77795967deddd7a08b40718/raw/sudoku_solver_seed.py"
candidate_str = urlopen(seed_solver_url).read().decode("utf-8")
```
```python
evaluate(candidate_str, df.iloc[0])
```
```
(0.0014285714285714286,
{'correct': True,
'time': 0.010603091039229184,
'num_lines': 105,
'time_score': 0.0,
'brevity_score': 0.0095})
```
```python
evaluate(candidate_str, df.iloc[12])
```
```
(0.6947964340601382,
{'correct': True,
'time': 0.0018427310278639197,
'num_lines': 105,
'time_score': 0.8157,
'brevity_score': 0.0095})
```
Interestingly, everything up to this point was completely independent of GEPA itself. It was pure Python. It really shows the nice API design, that we can do these things completely independent of the actual framework.
Now we have to make sure that GEPA is actually installed and has the latest version 0.1.0.
```python
!pip install gepa --upgrade
```
```python
import gepa.optimize_anything as oa
```
```python
from gepa.optimize_anything import GEPAConfig, EngineConfig, ReflectionConfig
```
Now we come to the main function of `optimize_anything`, which takes in our seed candidate, our evaluation function, as well as our training and validation data sets, and optional strings which describe the objective as well as some background to the optimization system in plain language.
It also takes in a GEPA config instance, which lets us configure things like the LLM we'll use for optimization as well as the maximum number of metric calls, basically the maximum number of iterations to control the cost.
We will use GPT-5.2 as the LLM for optimization and we will do a maximum of 500 metric calls.
That's all it takes. As you can see the actual GEPA API is very lean.
Let's run it now (may take 5–10 minutes and should cost around $0.2 - $0.3).
```python
result = oa.optimize_anything(
seed_candidate=candidate_str,
evaluator=evaluate,
dataset=train_df.to_dict('records'),
valset=val_df.to_dict('records'),
objective="Optimize a Python Sudoku solver for maximum speed while maintaining 100% correctness. The solve() function takes an 81-char puzzle string ('.' for blanks) and returns an 81-char solution string.",
background="The seed solver uses numpy arrays and constraint propagation (naked singles, hidden singles) with backtracking.",
config=GEPAConfig(
engine=EngineConfig(max_metric_calls=500),
reflection=ReflectionConfig(reflection_lm="openai/gpt-5.2"),
),
)
```
Here is an AI-based summary of the run:
**8 iterations, 534 evaluator calls, 6 candidates explored**
| Candidate | Val Score | Approach |
|-----------|-----------|----------|
| 0 (seed) | 0.072 | Your original numpy solver |
| 1 | 0.269 | Bitmask + MRV + trail-based backtracking |
| 2 | 0.245 | Bitmask + propagation queue + copy-based backtracking |
| **3 (best)** | **0.322** | Bitmask + MRV + least-constraining value heuristic |
| 4 | 0.238 | Similar to candidate 5, numpy-based bitmask |
| 5 | 0.249 | Recursive assign/eliminate with hidden singles |
The best candidate (#3) is about **4.4× better** than your original solver on the scoring metric. The key improvements GEPA found:
- **Dropped numpy entirely** — pure Python lists + bitmasks
- **9-bit candidate masks** instead of numpy arrays for tracking possibilities
- **Trail-based undo** instead of copying grids (faster backtracking)
- **Least-constraining value** heuristic when branching (for cells with 3+ candidates)
- **Precomputed lookup tables** (POPC, LOWDIG, DIGITS) for fast bit manipulation
Note that many puzzles (especially the hardest ones) still score near 0 — those take >10ms so the time score bottoms out.
And here is the code for the best solver our system came up with:
You can find the full optimized solver here: [GitHub Gist – `sudoku_solver_optimized.py`](https://gist.github.com/vacmar01/c677bc96c96224dce77b926184fef9f7).
Let's also look at how it holds up against the baseline on a random example from our dataset:
```python
evaluate(result.candidates[3]["current_candidate"], df.iloc[12])
```
```
(0.8388610768309542,
{'correct': True,
'time': 0.00013641000259667635,
'num_lines': 329,
'time_score': 0.9864,
'brevity_score': 0.003})
```
```python
evaluate(candidate_str, df.iloc[12])
```
```
(0.6866624460475785,
{'correct': True,
'time': 0.0019384250044822693,
'num_lines': 105,
'time_score': 0.8062,
'brevity_score': 0.0095})
```
As you can see, the best candidate is about an order of magnitude faster, but also has about 3× as many lines of code.
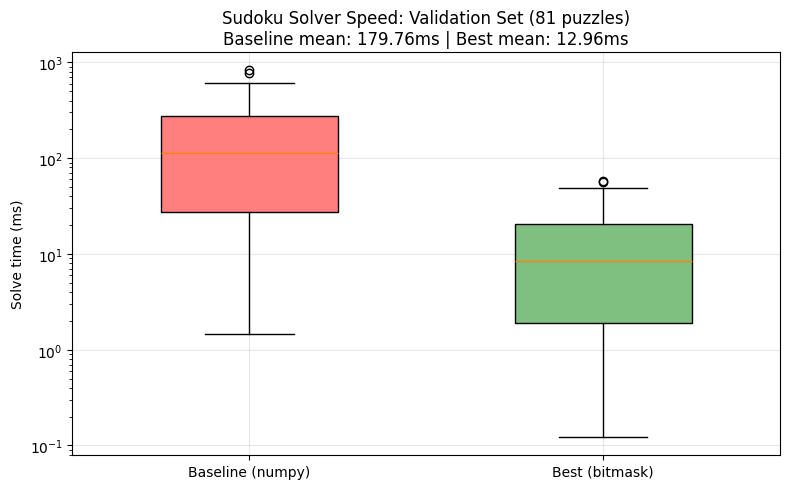
As you can see, it's super easy to optimize text-based artifacts using the new API of GEPA.
And this really makes me super excited because before you had to basically buy into the whole DSPy universe to get the advantages of reflective prompt optimization and these optimizations were mostly confined to prompts.
But now it's agnostic not only to how you build your system, but also to the kind of text-based artifact you're optimizing.
You can truly optimize anything with it. There are so many things I'm currently thinking about, like optimizing SQL queries against a real database or even optimizing agent prompts/skill files to finish tasks with as few tokens as possible.
The possibilities here are truly endless, and I'm super excited to see what this new release really enables us to do.
I think it's a very fundamental step forward.